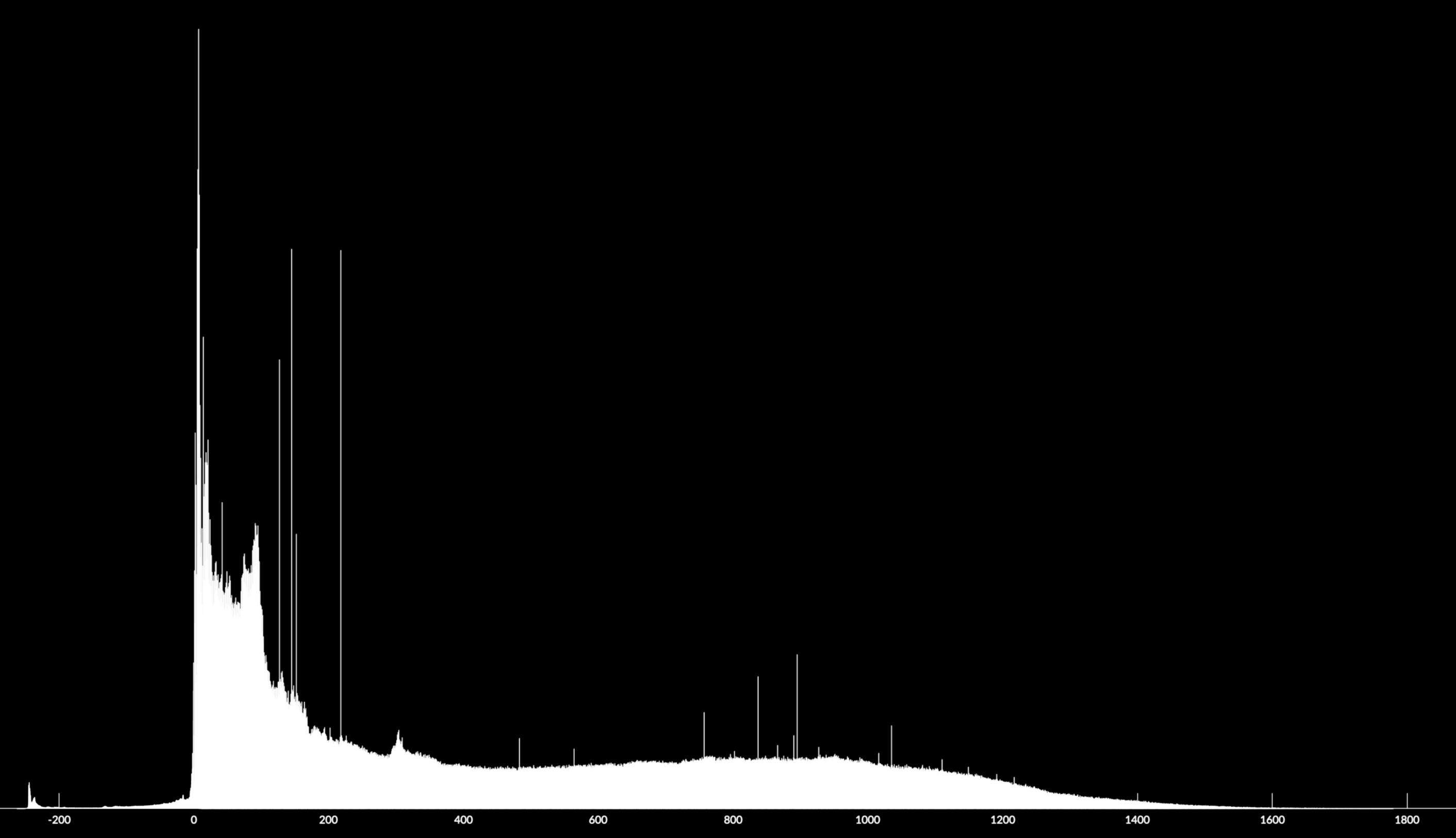
#006 - Anomalies in sea level
Shown here is a histogram of the elevations per pixel from the surface interpolator described in post #005, for the whole basin (including mountain peaks) of Burrard Inlet. Within the bounds of the model (From 49.226 to 49.5 latitude and from -123.3 to -122.8 longitude) elevations span from -267m underwater to 1779.5m at mountain peaks. However, the most common elevations cluster around 0m, or sea level at low tide.
A special implementation of the surface interpolator can use non-lattice points over which the kernel moves, for example, to study elevation variance of specific features. In this case, points are taken from four different shoreline contours of Burrard Inlet, one for the high water mark and three for elevation depths, at 0m, 2m and 5m underwater. All of these contours are shapefiles created by the Canadian Hydrographic Service.
Let’s explore the high water mark first. Shown above in blue is the deconstruction of the shoreline starting at Point Atkinson and closing at Point Gray, with vertical lines showing the bounds of different regions in the inlet. In red is the running mean, so the general trend is visualized more clearly. Even though the median high water mark lies at 4.59m above sea level, there is a lot of variance, with the mean at 3.67m and a standard deviation at a staggering ±5.26m. This strong anomaly, or jitter, in elevation is likely due to the nature of the high water mark, which is not based on sea level at an altitude, but on the visual limit of water at high tide.
Here the high water mark (yellow) is compared to underwater contours at 0m depth (green), 2m depth (blue), and 5m depth (purple). Each has three running means at different levels of coarseness, to highlight the elevation jitter. The contour for 0m, or sea level, has its median at -0.35m, mean at -0.44m, with a standard deviation of ±2.54m. This means that the line that delimits the low tide has an error of almost 3 meters, an improvement on the high water mark jitter, but still quite troublesome. Next is the contour at 2m depth, with median at -2.23m, mean at -2.41m, with a standard deviation of ±1.39m. This hints that deeper shorelines that mark extreme low tides have more consistent profiles and less jitter error, shown with the standard deviation decreasing as depth increases. Finally, the perpetually underwater contour at 5m depth has its median at -5.11m, mean at -5.22, and standard deviation at ±1.36m, the most consistent of all the shorelines.
Ahown above is alternative visualization of the high water mark and depth contours using histograms. There is an inverse relation between elevation anomaly and depth, perhaps because the upper layers are much more energetic and weather-driven. This high energy, coupled with the capricious geometry of a fjord basin, can create localized clusters of tidal waters well above sea level, that are then marked as high water. This phenomenon is important to consider when addressing shoreline change, especially in the context of climate change and global sea level rise.
